Compressed Sensing example¶

We set up a linear forward model using a Fourier matrix as dictionary and reconstruct the underlying sparse vector from linear projections using a matrix with elements drawn randomly from a Gaussian distribution.
import numpy as np
import matplotlib.pyplot as plt

import fastmat as fm
import fastmat.algorithms as fma

# Problem dimensions
compression_factor = 4
N = 60  # Problem size
M = int(N / compression_factor)  # Number of observations
k = 3  # sparsity level
noise_power_db = -10.

# Ground truth of scenario
# We choose the ground_truth to be two dimensional here to align all vectors
# explicitly vertical, allowing easy stacking later on
ground_truth_positions = np.random.choice(N, k)
ground_truth_weights = np.random.randn(k, 1)
ground_truth = np.zeros((N, 1))
ground_truth[ground_truth_positions] = ground_truth_weights


# Set up the linear signal model and reconstruction method,
# consisting of Measurement Matrix `Phi` and Signal Base `Dict`
Phi = fm.Matrix(np.random.randn(M, N))
Dict = fm.Fourier(N)

A = Phi * Dict


# Now determine the actual (real-world) signal and its observation
# according to the specified Measurement matrix and plot the signals
# also allow for noise


def add_noise(signal, pwr_db):
    return signal + 10**(pwr_db / 10.) * np.linalg.norm(signal) * (
        np.random.randn(*signal.shape) / np.sqrt(signal.size)
    )


x_clean = Dict * ground_truth
x = add_noise(x_clean, noise_power_db)
b = Phi * x

# Now reconstruct the original ground truth using
# * Orthogonal Matching Pursuit (OMP)
# * Fast Iterative Shrinkage Thresholding Algorithm (FISTA)
# * Soft-Thresholding with simplified Exact Line search Algorithm (STELA)
numLambda = 5
numSteps = 600
alg_omp = fma.OMP(A, numMaxSteps=k)
alg_fista = fma.FISTA(A, numMaxSteps=numSteps, numLambda=numLambda)
alg_stela = fma.STELA(A, numMaxSteps=numSteps, numLambda=numLambda)
y_omp = alg_omp.process(b)
y_fista = alg_fista.process(b)
y_stela = alg_stela.process(b)

# Setup a simple phase transition diagram for OMP, for a number of randomly
# chosen measurement matrices and another number of noise realizations for
# each measurement matrix.
trials = 15
M_phase_transition = np.arange(k, N)
true_support = (ground_truth == 0)
success_rate = np.zeros(len(M_phase_transition))
for index, m_phase_transition in enumerate(M_phase_transition):
    for _ in range(trials):
        # randomly choose a new measurement matrix
        Phi_pt = fm.Matrix(np.random.randn(m_phase_transition, N))
        alg_omp = fma.OMP(Phi_pt * Dict, numMaxSteps=k)

        # randomly choose `trials` different noise realizations
        x_pt = add_noise(np.tile(x_clean, (1, trials)), noise_power_db)
        b_pt = Phi_pt * x_pt

        # and process recovery all in one flush
        recovered_support = alg_omp.process(b_pt)

        # now determine the success of our recovery and update the success rate
        success = (recovered_support == 0.) == true_support
        success_rate[index] += np.mean(np.all(success, axis=0))

    print(success_rate[index])

# finally, normalize the success_rate to the amount of trials performed
success_rate = success_rate / trials

# Plot all results
plt.figure(1)
plt.clf()
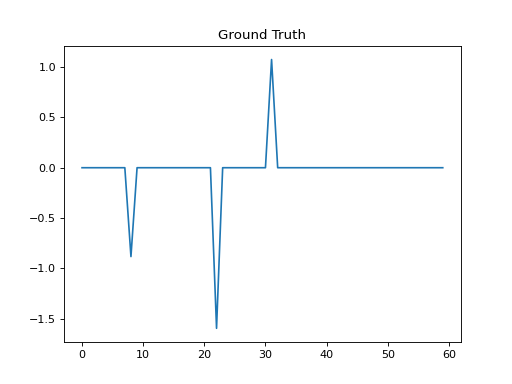
plt.title('Ground Truth')
plt.plot(ground_truth)

plt.figure(2)
plt.clf()
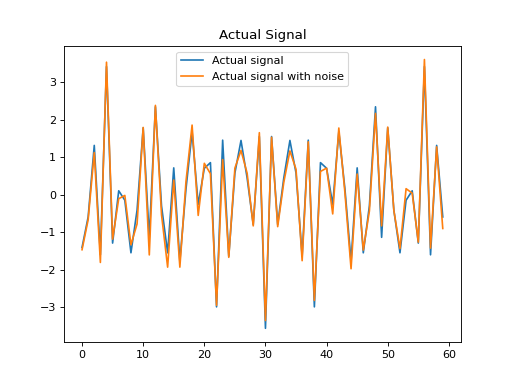
plt.title('Actual Signal')
plt.plot(x_clean, label='Actual signal')
plt.plot(x, label='Actual signal with noise')
plt.legend()

plt.figure(3)
plt.clf()
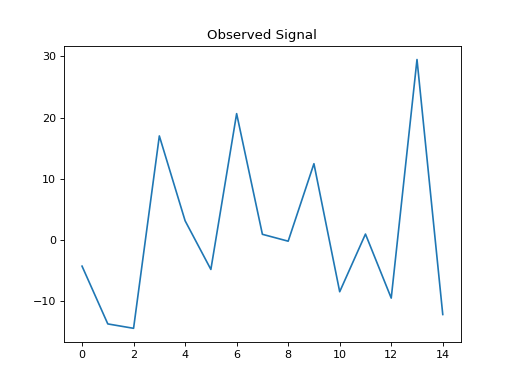
plt.title('Observed Signal')
plt.plot(b)

plt.figure(4)
plt.clf()
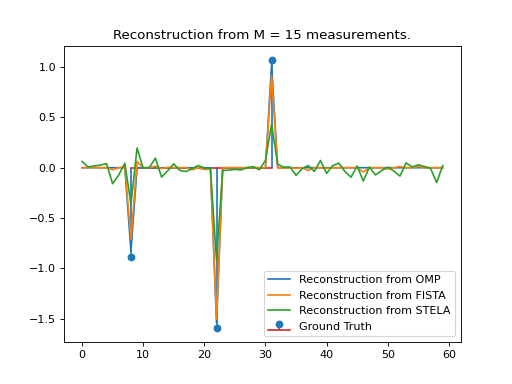
plt.title("Reconstruction from M = " + str(M) + " measurements.")
plt.stem(ground_truth_positions, ground_truth_weights, label='Ground Truth')
plt.plot(y_omp, label='Reconstruction from OMP')
plt.plot(y_fista, label='Reconstruction from FISTA')
plt.plot(y_stela, label='Reconstruction from STELA')
plt.legend()
#
plt.figure(5)
plt.clf()
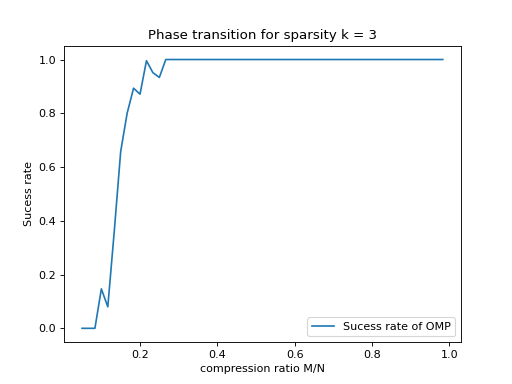
plt.title("Phase transition for sparsity k = " + str(k))
plt.plot(1. * M_phase_transition / N, success_rate, label='Sucess rate of OMP')
plt.xlabel('compression ratio M/N')
plt.ylabel('Sucess rate')
plt.legend()
plt.show()
(Source code)